Secret of Chocolate Poles

Time Limit : 1 sec, Memory Limit : 262144 KB

Problem A Secret of Chocolate Poles

Wendy, the master of a chocolate shop, is thinking of displaying poles of chocolate disks in the showcase. She can use three kinds of chocolate disks: white thin disks, dark thin disks, and dark thick disks. The thin disks are 1 cm thick, and the thick disks are k cm thick. Disks will be piled in glass cylinders.

Each pole should satisfy the following conditions for her secret mission, which we cannot tell.

• A pole should consist of at least one disk.
• The total thickness of disks in a pole should be less than or equal to l cm.
• The top disk and the bottom disk of a pole should be dark.
• A disk directly upon a white disk should be dark and vice versa.

As examples, six side views of poles are drawn in Figure A.1. These are the only possible side views she can make when l=5 and k=3.

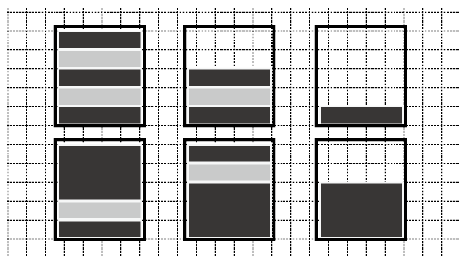
Figure A.1. Six chocolate poles corresponding to Sample Input 1

Your task is to count the number of distinct side views she can make for given l and k to help her accomplish her secret mission.

Input

The input consists of a single test case in the following format.

l k

Here, the maximum possible total thickness of disks in a pole is l cm, and the thickness of the thick disks is k cm. l and k are integers satisfying 1≤l≤100 and 2≤k≤10.

Output

Output the number of possible distinct patterns.

Sample Input 1

5 3

Sample Output 1

6

Sample Input 2

9 10

Sample Output 2

5

Sample Input 3

10 10

Sample Output 3

6

Sample Input 4

20 5

Sample Output 4

86

Sample Input 5

100 2

Sample Output 5

3626169232670

---

Source: ACM International Collegiate Programming Contest , Asia Regional Tsukuba, Tsukuba, Japan, 2017-12-17 

 

题意：有三种盘子，1 cm厚的黑盘，1 cm厚的白盘，和 k cm厚的黑盘，最上面和最下面一定是黑盘，同颜色的盘子不能相邻，总厚度在 l cm 以内有多少种放法；

 

以黑盘个数做标记，忽略厚度不同，共有 (l+1)/ 2 种方法，每种再用厚盘替换普通黑盘，可以替换 1~ i 个，写个组合数就行了；

#include 
    
     #include 
     
      #include
      
       using namespace std;long long int c(long long m,long long n){    long long ans=1;    for(long long k=1; k<=n; k++)    {        ans=(ans*(m-n+k))/k;    }    return ans;}int main(){    long long  l, k;    while(cin >> l >> k)    {        long long  i, j;        long long sum = 0;        for( i=1; i<=(l+1)/2; i++)        {            sum++;            for( j=1; j<=i; j++ )            {                if( i-j+k*j + i-1 > l) break;                sum += c(i,j);            }        }        printf("%lld\n",sum);    }    return 0;}